EARTHQUAKE, ITS EFFECTS, DESIGN CONSTRUCTION OF BUILDINGS
Prof. Y. P. Gupta,
Chairman, ICI UP Allahabad Center & Materials Consultant, BCEOM-LASA JV Allahabad By Pass Project
INTRODUCTION
Earthquake is a natural phenomenon, which can occur any time anywhere. Therefore, the Buildings must be built in such a way that they are safe during such occurrence. IS: 1893, Code Of Practice For “CRITERIA FOR EARTHQUAKE RESISTANT DESIGN OF STRUCTURES” give the guidelines for the design of structures. This has been revised (2002) taking care of the experiences of several Earthquakes, which occurred after 1984 when the code was last revised. During various Earthquakes, large number of buildings failed and many lessons are learnt especially after Gujrat Earthquake (2001). This paper describes in brief the phenomenon of Earthquakes, various provisions that can be made for calculating the Design forces. It also brings out many provisions, which can be implemented in design and/or construction of buildings to make them earthquake resistant.
HOW EARTHQUAKES OCCUR ?
Earth is a Spherical body made up of mainly four layers consisting of Inner & Outer Core, Mantle and Crust as shown in Figure 1. The Core of Earth is very hot. There is enormous temperature and pressure gradient between Core (innermost layer) and Crust (outermost / top layer), which generates convection currents in the Mantle. These currents cause the Crust and a portion of the Mantle to slide over the outer Core. It also gives rise to the development of strain energy, which causes crust to slide over mantle. Earth’s crust consists of 7 major tectonic plates (that contain continents and ocean basins), which keep moving in different directions. As a result of such movements, strains are building up at plate interfaces. In course of time, when this cumulative strain energy becomes excessive for the rock plates to sustain, it gets released in the form of a slip occurring between adjoining plates. The interface of plates is called fault or fault zones. Some of these faults are active, whereas others are not. When the amount of energy stored inside Earth’s body increases and exceeds the breaking strength of the Earth’s crust in a active fault zone, then it suddenly breaks and releases the energy stored inside the Earth causing vibrations or Earthquake. There are many other explanations about the occurrence of earthquakes.
Tsunami
When the epicenter of earthquake is on Sea floor, then vibrations are also caused on the body of seawater. Therefore, earthquakes on sea floor are the origin of tsunami waves. After an earthquake has occurred beneath the sea floor at shallow depth, it takes some time (say few minutes to few hours) for dynamic waves of large heights to be formed. The shock embedded wave travels at a speed of about 1000 km per hour or so and reaches Coastline.
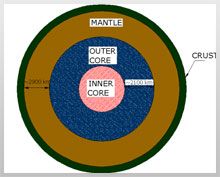
Fig. 1 – Earth’s Core & Crust Showing 4 Layers of Earth’s Body
MAGNITUDE AND SCALE OF AN EARTHQUAKE
Rupture of earth’s crust generally commences at a deep point, somewhere inside the Earth’s body on the fault plane, which is called Focus or Hypocenter of the quake. At this point, the first rupture of the fault surface takes place. The point right above the focus is called the Epicenter as shown in Figure -2. The magnitude of an earthquake is the measure of the energy released from the Focus. It is commonly measured in terms of Richter’s scale.
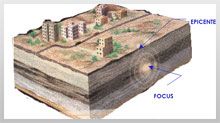
EPICENTER FOCUS Fig. 2 – Typical Position of Epicenter & Focus (Hypocenter) inside earth’s body
The relation between the energy released and magnitude is: Log E = 11.8 + 1.5 M Where,
M – Magnitude of earthquake
E – Amount of energy released during an Earthquake.
By definition, Magnitude is the logarithm to the base 10 of the maximum trace amplitude, measured in microns (10-6 m), which the Standard Short Period Torsion (Wood – Anderson) Seismometer would register due to the earthquake at an epicentral distance of 100 km.
It is seen from above relation that energy released by an earthquake increases by a factor of 32 for each unit increase in magnitude. That is, each increase in magnitude number is a 10 – fold bigger wave and has 32 – fold increase in energy released by that wave. It is said that Bhuj Earthquake (2001) at magnitude 7.7 released so much energy, which was about 100 times the energy given by Atom Bomb dropped on Hiroshima during World War II. The magnitude of earthquake by itself is not sufficient to indicate whether Structural damage at any place can be expected. This is only a measure of the size of earthquake and energy released at its source. The effect of an earthquake in an area depends on the distance of the structure from the focus and nature of the Earth’s crust at the location of the Structure. Thus, how an individual, positioned on the earth’s surface in different parts of the World, feels the severity of an Earthquake is called Earthquake Intensity. This is a measure of damage occurred to a structure and is defined by Modified Mercalli Scale. The intensities are classified on 12 level scales in IS: 1893-2002 ranging from bare minimum to total destruction of structure.
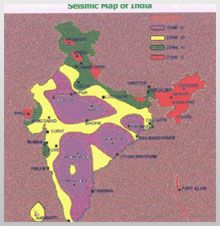
SEISMIC ZONING MAP OF INDIA
As per IS: 1893 – 2002 Pt I code of practice for “Criteria for Earthquake Resistant Design of Structures”, India is now divided into four earthquake zones as shown in Figure – 3. In this revision, Zone I has been eliminated. Some areas of Zone II like Killari area in Maharastra etc have been upgraded and shifted to Zone III. Approximately 12 percent of India (Bhuj, Jammu and Kashmir, Uttaranchal, the North-East, north Bihar and Andaman and Nicobar Islands, etc) falls under the seismic zone V – the highest risk category.
EFFECT OF EARTHQUAKE ON BUILDINGS
Earthquakes directly effects ground shaking and in turn can generate Landslides, Tsunamis, Liquefaction of ground and may also cause damage tostructure by way of shaking etc. Structural response affecting the buildings is described here.
Fig. 3 – Seismic Zoning Map of India – The four Earthquake Zones (IS: 1893-2002)
Why does a Building Collapse?
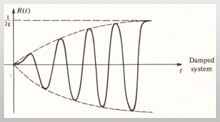
The response of a Structure to an Earthquake is a function of the nature of the foundation soil; material, form, size & mode of construction; and the duration and characteristics of ground motion. A typical response of any building during an Earthquake is shown in Figure – 4(a). This response depends on the natural period of vibration & absorbing Character (damping) of the structure. During an earthquake, amplitude of vibration generally buildup in a few cycles. A typical diagram showing the amplitude build up of any object during few cycles of earthquake excitations
Effect of earthquake on some of the buildings during Latur (1993) and Gujrat (2001) earthquakes is shown in figures-5 & 6, as few typical examples of structural behavior. It is to be noted that RC framed buildings during Latur Earthquake suffered less damage as compared to the Gujrat Earthquake. This may be because of poor quality of design / construction and absence of proper beam column connections in the Gujrat area.
Earthquakes cause motion to the ground in random direction. The horizontal vibration is predominant & more damaging. The amplitude of motion of any structure normally builds up over a period of time in a few cycles i.e. duration of Earthquake as shown in Figure -4(b). Thus, if the Earthquake lasts longer, the amplitude of vibration is more, i.e. the structure will deflect more and get damaged.
The violent ground motion pushes the building rapidly from one direction to another making it difficult for the super-structure to constantly balance its load due to inertial effects. Result: while columns can bend, the swaying motion, when intensified, snaps the building like matchsticks and collapses.
A superstructure can be damaged, not only on account of the shaking which results from quakes but also due to chain effects like fire, land slide etc caused by earthquake.

Fig. 5(a) – An undamaged Reinforced Concrete building after the Latur Earthquake

Fig. 5(b) – A RC Hospital Building suffered only diagonal cracking in the walls during the Latur Earthquake (1993).
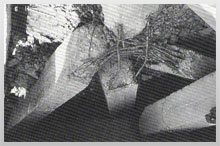
Fig. 5(c) -A beam-column junction in a multi – storied building failed during the Latur Earthquake (1993) – Bad placement of reinforcement at the junction.

Fig. 6(a) – A RC apartment building in Ahemdabad failed during the Gujrat Earthquake (2001) – Bad design
HOW TO MAKE BUILDING QUAKE RESISTANT ?
There are two essential features to make a building earthquake resistant i.e. safe design and quality construction. To achieve this, the desirable factors required in design of any structure for better Earthquake resistance are:
* Stiffness / Ductility and
* Damping.
The stiffness is an ultimate effect of structural design & material characteristics while ductility and damping comes directly from material used for construction. Thus, it is desirable that the material used for construction is ductile, especially at locations where damage is expected like at Beam-Column junction. Normally Reinforced Concrete is a good ductile material.
CHOICE OF CONSTRUCTION MATERIALS
A) Reinforced Concrete
Construction material is crucial for the earthquake resistance and durability of structure. The safest building will be the one made of all steel (though very heavy – attracting more earthquake force), as it is an extremely strong material. Reinforced Concrete is the next most suitable material for earthquake resistant construction of buildings. It is a good, durable and economic material of construction, but the condition is that the quality of construction should be good. It was seen during the Latur earthquake, that most buildings made with concrete, remained standing without suffering much damage. But during the Gujrat earthquake many buildings made in RCC also got damaged or collapsed because of poor quality of construction.
B) Other Materials
A brick, stone or mud house cracks even with moderate tremors. However, these materials can be effective when strengthened with RCC elements at critical points. Masonry buildings become brittle when large deflections take place, so RCC bands can strengthen them at regular intervals. A wooden frame building is good as it absorbs shock evenly and vibrates along the quake and unlikely to collapse. The danger with wooden frame structures is that it is highly inflammable and has limited use i.e. only up to one or two stories.
DESIGN OF BUILDINGS FOR EARTHQUAKE EFFECT
The behavior of a building during ground vibration is a function of the nature of foundation soil and natural period of vibration of the structure, which depends on the material used in construction, its form, size, and mode of construction etc. The structure also gets affected with the duration & intensity of the earthquake. IS: 1893 -2002 specifies seismic coefficients for calculating the design forces for simple structures standing on soil which will not settle or slide much, due to loss of strength (like Liquefaction effect). In the design of buildings, horizontal force due to earthquake is considered simultaneously along with the vertical forces.
Normally, the natural period of vibration of any structure should not coincide with the predominant period of earthquake excitations, otherwise resonance may occur and even the strongest structure may collapse. Thus, while designing the building, following aspects should be looked into:
a) Magnitude & Type of Earthquake Excitations.
b) Natural Period of Vibration of Structure along with its material & mode of construction. Response of Structure to earthquake Design forces, to which the building elements will be subjected, can be calculated by any one of the following methods.
1. Seismic Coefficient Method
2. Response Spectrum Method (Modal Analysis)
3. Time History Analysis.
Depending upon the complexity and importance of Structure, any one of the above three methods can be adopted. Here only seismic coefficient method is described, as this is the most common method. Earthquake forces can be calculated in any direction of Structure, but the most damaging direction is horizontal (Least lateral direction).
The horizontal earthquake force can be calculated as:
VB (or F) = Ah W -¦..(1)
Where,
VB (or F) = Total Design force generated due to earthquake or Design Seismic Base Shear
W = Seismic weight of the Building i.e. Sum of the Seismic weight of all floors (DL + appropriate amount of live load as per IS: 1893)
Ah = Design horizontal seismic coefficient.
Vertical acceleration coefficient, Av can be taken as 2/3 Ah
I. SEISMIC COEFFICIENT METHOD (AS PER IS: 1893 – 2002)
The Design Horizontal Seismic Coefficient Ah for a structure is determined by the following expression as per IS: 1893 – 2002:
Ah = (Z/2) x (Sa/g) / (R/I) -¦(2)
Subject to the condition that for any Structure having T 0.1 sec, Ah will not be less than Z/2 for any value of I/R. Here description of various parameters is given below.
a) Seismic Zone Factor, Z:
The Values of Seismic Zone Factor Z reflect more realistic values of effective peak ground acceleration under maximum considered earthquake (MCE) in each Seismic Zone. These values are given in table 1 as per revised 1893 code. The factor 2 in the denominator of Z is used so as to reduce the maximum considered earthquake (MCE) zone factor to the factor for design basic earthquake factor (DBE).
Table: 1 Seismic Zone Factor, Z
| Seismic Zone | II | III | IV | V |
| Seismic Intensity | Low | Moderate | Severe | Very severe |
| Zone Factor | 0.1 | 0.16 | 0.24 | 0.36 |
Zone factors for some important cities have also been modified. These are given in Annexure E of the code. For example for Lucknow , Kanpur etc, it is 0.16.
Response reduction factor, R, depending on the perceived seismic damage performance of the structure is characterized by ductile or brittle deformations, with the condition that the ratio (I/R) shall not be greater than 1.0 d) Average Acceleration Response Coefficient, Sa/g: The acceleration response of a structure to ground vibrations is a function of the nature of foundation soil, material, size and mode of construction of structure and characteristics of ground motion. The Response Spectra is now specified for three types of foundation strata viz. one for Rock or hard soil, second for Medium Soil and third for soft Soil, as given in three different curves of Figure -7. Fill type of soil is not considered suitable for construction activity in earthquake zones.
d) Average Acceleration Response Coefficient, Sa/g:
The acceleration response of a structure to ground vibrations is a function of the nature of foundation soil, material, size and mode of construction of structure and characteristics of ground motion. The Response Spectra is now specified for three types of foundation strata viz. one for Rock or hard soil, second for Medium Soil and third for soft Soil, as given in three different curves of Figure -7. Fill type of soil is not considered suitable for construction activity in earthquake zones.
Table: 2- Some Values of Response Reduction Factor “R” for Building Systems
| S. No. | Lateral Load Resisting System | R | |
| A. | Building Frame System Alone | ||
| 1. | Ordinary RC Moment-Resisting Frame | 3 | |
| 2. | Special RC Moment-Resisting Frame | 5 | |
| 3. | Steel Frame with Concentric Braces | 4 | |
| 4. | Steel Frame with Eccentric Braces | 5 | |
| 5. | Steel Moment Resisting Frame | 5 | |
| B. | Load Bearing Masonry Wall Buildings | ||
| 1. | Un-reinforced | 1.5 | |
| 2. | Reinforced with horizontal RC Bands | 2.5 | |
| 3. | Reinforced with horizontal RC Bands and vertical bars at Corners & Jambs | 3 | |
| C. | Ordinary Reinforced Concrete Shear Walls | 3 | |
| D. | Ductile Shear Walls | 4 |
The average acceleration response coefficient Sa/g, for 3 types of soil sites as given in Figure- 7, is based on the appropriate natural period and 5% damping value of the structure. Natural period of vibration can be calculated by usual methods or as given below for multi-story building. A normal structure in concrete will have a damping value of about 5% for which the curves are given. For other damping values, a multiplying factor is given in IS: 1893, and reproduced here in Table – 3. Some empirical relations can also give values of Sa/g .
Fig. 7 – Shape of Response Spectra curves at 5% Damping Level

Table 3- Multiplying Factor for Other than 5% Damping level
| % Damping | 0 | 2 | 5 | 7 | 10 | 15 | 20 | 25 | 30 |
| Factor | 3.20 | 1.40 | 1.00 | 0.90 | 0.80 | 0.70 | 0.60 | 0.55 | 0.55 |
E) Building Category:
After finding the values of all parameters given in equation 2, the value of Ah can be found. Then depending upon the value of seismic Coefficient, Ah, the category of Building can be defined as given in Table 4.
Table 4 – Classification of Building Categories
| Range Of Ah | Building Category |
| Less than 0.05 | A |
| 0.05 to 0.06 | B |
| 0.06 to 0.08 | C |
| 0.08 to 0.12 | D |
| > 0.12 | E |
APPROXIMATE RELATIONS FOR FUNDAMENTAL PERIOD OF VIBRATION
The empirical expression for estimating the fundamental natural period “T” of multistory buildings having regular moment resisting frame can be found by following relations (as given in IS: 1893):
a) The approximate fundamental natural period of vibration “T” of moment resisting frame buildings without brick infill panels is: Ta = 0.075 h 0.75 – for RCC frame Building -¦3(a) = 0.085 h 0.75 – for Steel frame Building -¦3(b)
b) The approximate fundamental natural period of vibration “T” of all other buildings including moment resisting frame buildings with brick infill panels may be estimated by: Ta = 0.09 / d -¦4 Where, Ta = Fundamental period of vibration in seconds h = Height of Building in meters. D = Base dimension of building at plinth level in “meters”, along the considered direction of the lateral force.
